凹函数的性质是什么?大学微积分:什么函数既凸又凹?凹函数和凸函数有什么区别?什么是凹函数及其属性?凹函数的特征如果f(x)是凹函数,那么-f (x)是凸函数,通常通过将凹函数转化为凸函数来研究。如何判断函数是凸的还是凹的?如果f(x)是凹函数,那么f(x)是凸函数,通常通过将凹函数转化为凸函数来研究。
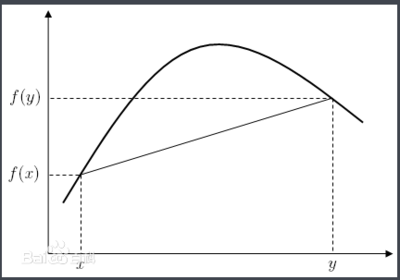
1、上凸函数就是下凹函数吗?
凸函数就是凹函数,因为凸函数就是凹函数。如果定义在一个区间上的一元实函数是连续函数,并且对于这个区间上的任意两点X1和X2,当X1”时,称为严格凹函数或严格凸函数。如果f(x)是凹函数,那么f(x)是凸函数,通常通过将凹函数转化为凸函数来研究。
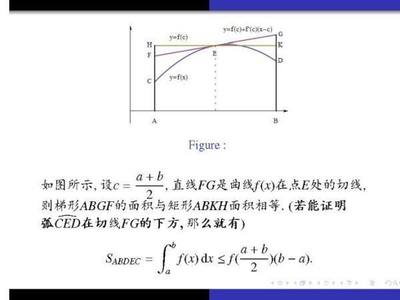
如果c是闭区间,那么f在c. 2的末尾可能是不连续的。一元可微函数在某个区间上是凸的当且仅当它的导数在该区间上是单调的。3.一元连续可微函数在区间上是凸的当且仅当该函数在其所有切线之上:对于区间上的所有x和y,存在f (y) > f (x) f (x) (yx)。特别地,如果f(c)0,那么c是f(x)的最小值。
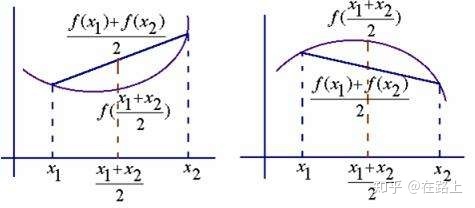
2、如何判断一个函数是凸函数或是凹函数?
在可微函数的情况下,如果一阶导数在区间内连续增加,则是凹函数;形象地说,就是开口向上,反之,就是凸函数;因为一阶导数连续增加,凹函数的二阶导数大于0;因为一阶导数连续减小,凸函数的二阶导数小于0。凸函数是:缓慢上升,快速下降;凹的作用是:慢减快增。定义:f ((x y)/2) > (f (x) f (y))/2是凸函数,反之亦然。
设f(x)定义在区间I中,f(x)称为区间I中的凸函数当且仅当:I上任意两点X1。
